This is going to be a cosmology post. It will take a while to get up.
First some credit to Ned Wright, prof of Cosmology at UCLA. I'm mostly just trying to understand and interpret his excellent tutorial web site.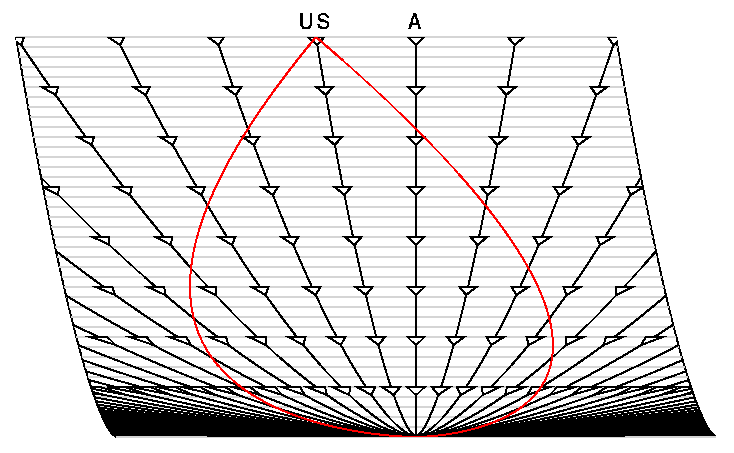
First some credit to Ned Wright, prof of Cosmology at UCLA. I'm mostly just trying to understand and interpret his excellent tutorial web site.

Ok, here we go. Beginning with a picture from the tutorial...
What we see above is a pitcure of the universe! Time is the up-down dimension and distance is the right left dimension. Each of the (almost) straight black lines is for a different observer, at a different place in the universe. Each of the different observers is moving away at a different speed, harking back to the big bang at the bottom when they were all colocated.
"Moving away from where?" you can ask, and the answer is "From me!" ...or from anyone. All viewpoints in the regularly expanding universe are equivalent. He shows that by skewing the frame of reference in this picture. The observer at "A" feels he is unmoving, so his line of position over time is straight, whereas the line showing "us" has relative motion.
There's a lot more to say by way of explaining this diagram, and I will try to get to it soon, but want to get my questions down first.
1) If it's the same for all observers, then everyone should see the same thing, right? That means both we and A should see the same CMB radiation, though we have dramatically different velocity. It is tempting here to say different absolute velocity but is there such a thing? If there's absolute velocity vs CMB, then there's a center: a preferred location in the universe and the point of this diagram is that that's not so. But (here's the question at last) if there is no preferred center, then there is no absolute velocity, and then seemingly none should be measured, by anyone, vs the CMB. Yet there is a dipole! Why? I think this has to be due to a recent velocity, an acceleration that has us moving relative to our local chunk of space. If it were secular (for all time) then we'd be in a different chunk of space (and seeing uniform CMB).
2) The picture shows "light cones" as little triangles along everyone's timeline. That's how fast a signal would travel if you emitted it. You could imagine adjacent societies communicating by radio, with delays for their successive messages (light cones) to reach each other. This elegant picture shows how the light from the big bang can reach us, after a long journey and an uphill race against the expanding universe wherein it actually loses ground before finally approaching us. That's the red pear shape. This explanation makes perfect sense to me if I think of it as an explosion in air. Everywhere, sound moves at the speed of sound, but the air through which it travels moves at different velocities depending on which part of the explosion each pocket of air is located in. As such the sound speeds up or slows down (in a coordinate frame fixed to the location of the original explosion). This all works perfectly for air, but air is the aether through which sound moves. Is there then aether for light? What if there is nobody there to measure the light as it travels from its source to us, through the intervening universe? Is it still doppler shifted along the way, or is it meaningless to talk about a doppler without an observer? Does it arrive along the same trajectory, covering the same distance in the same time?
I think the answers are: the light behaves the same whether there's someone there to see it or not, there is no way to define redshift without an observer to be shifted "relative to" and so, yes, it covers the same trajectory. This is clearly about relativity, wherein the photons, and their speed, are invariant. The doppler changes depending on who (at what velocity vs the emitter) is observing at any given time. Again I'll mention the sound analogy works well (for me at least), so long as you assume that each timeline on the picture represents a different hunk of air.
Another way to learn something from the sound metaphor is to picture the interaction from the transmitter's perspective. We can speak (continuously!) to a nearby observer who, at the bang, suddenly begins travelling away at a huge speed. Thereafter, they and we hear each other with a huge redshift. We would both be speaking in ordinary time at ordinary rates but not just pitch but (consequently!) the time of arrival of words and sentences would be greatly stretched out. To each observer, the other appears to have slowed down. We can know this 'cause we can observe everyone's lips move at the speed of light. However in space, when the redshift is itself that of light, there is no meaning to the idea of the 3rd party observer in absolute or unmoving space. Also, I can be moving far faster than the speed of sound vs the transmitter, but the sound waves speed up as they refract through intervening blocks of atmosphere, each of which is successively travelling faster, with it's local bits of embedded shrapnel & flotsam. From the listener's perspective (measuring the sound pulse approaching via some kind of laser rangefinder) the sound is speeding up: you may think of the doppler as being applied incrementally and it IS, by the incremental delta velocities by all the air pockets. In space we don't know anything about the intervening observers (they may not be there!), but we "see" the light's redshift (as we would hear the doppler shift of sound) and so time at the observer seems to have been slowed down.

Have had fun watching the Sagan Cosmos shows this year, as Tyson is reprising them. I do think Sagan is better, but the point here is just to link to a cool picture, of Saturn. Maybe this will start a train of thought.
ReplyDelete